Practical Dependent Types: Type-Safe Neural Networks

Justin Le https://blog.jle.im (justin@jle.im)

Kiev Functional Programming, Aug 16, 2017

Preface

Slide available at https://talks.jle.im/kievfprog/dependent-types.html.

All code available at https://github.com/mstksg/talks/tree/master/kievfprog.

Libraries required: (available on Hackage) hmatrix, singletons, MonadRandom. GHC 8.x assumed.

The Big Question

The big question of Haskell: What can types do for us?

Dependent types are simply the extension of this question, pushing the power of types further.

Artificial Neural Networks

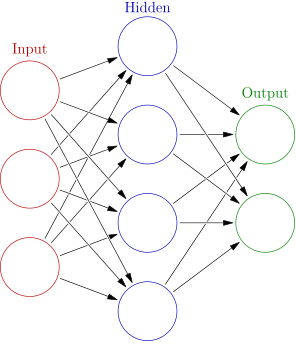
Feed-forward ANN architecture

Parameterized functions

Each layer receives an input vector, x : ℝn, and produces an output y : ℝm.

They are parameterized by a weight matrix W : ℝm × n (an m × n matrix) and a bias vector b : ℝm, and the result is: (for some activation function f)


y = f(Wx + b)

A neural network would take a vector through many layers.

Networks in Haskell

data Weights = W { wBiases :: !(Vector Double)  -- n
                 , wNodes  :: !(Matrix Double)  -- n x m
                 }                              -- "m to n" layer


data Network :: Type where
    O    :: !Weights -> Network
    (:~) :: !Weights -> !Network -> Network
infixr 5 :~

A network with one input layer, two hidden layers, and one output layer would be:

h1 :~ h2 :~ O o

Running them

runLayer :: Weights -> Vector Double -> Vector Double
runLayer (W wB wN) v = wB + wN #> v

runNet :: Network -> Vector Double -> Vector Double
runNet (O w)     !v = logistic (runLayer w v)
runNet (w :~ n') !v = let v' = logistic (runLayer w v)
                      in  runNet n' v'

Generating them

randomWeights :: MonadRandom m => Int -> Int -> m Weights
randomWeights i o = do
    seed1 :: Int <- getRandom
    seed2 :: Int <- getRandom
    let wB = randomVector  seed1 Uniform o * 2 - 1
        wN = uniformSample seed2 o (replicate i (-1, 1))
    return $ W wB wN

randomNet :: MonadRandom m => Int -> [Int] -> Int -> m Network
randomNet i []     o =    O <$> randomWeights i o
randomNet i (h:hs) o = (:~) <$> randomWeights i h <*> randomNet h hs o

Haskell Heart Attacks

  • What if we mixed up the dimensions for randomWeights?
  • What if the user mixed up the dimensions for randomWeights?
  • What if layers in the network are incompatible?
  • How does the user know what size vector a network expects?
  • Is our runLayer and runNet implementation correct?

Backprop

train :: Double           -- ^ learning rate
      -> Vector Double    -- ^ input vector
      -> Vector Double    -- ^ target vector
      -> Network          -- ^ network to train
      -> Network
train rate x0 target = fst . go x0
  where

Backprop (Outer layer)

    go :: Vector Double    -- ^ input vector
       -> Network          -- ^ network to train
       -> (Network, Vector Double)
    -- handle the output layer
    go !x (O w@(W wB wN))
        = let y    = runLayer w x
              o    = logistic y
              -- the gradient (how much y affects the error)
              --   (logistic' is the derivative of logistic)
              dEdy = logistic' y * (o - target)
              -- new bias weights and node weights
              wB'  = wB - scale rate dEdy
              wN'  = wN - scale rate (dEdy `outer` x)
              w'   = W wB' wN'
              -- bundle of derivatives for next step
              dWs  = tr wN #> dEdy
          in  (O w', dWs)

Backprop (Inner layer)

    -- handle the inner layers
    go !x (w@(W wB wN) :~ n)
        = let y          = runLayer w x
              o          = logistic y
              -- get dWs', bundle of derivatives from rest of the net
              (n', dWs') = go o n
              -- the gradient (how much y affects the error)
              dEdy       = logistic' y * dWs'
              -- new bias weights and node weights
              wB'  = wB - scale rate dEdy
              wN'  = wN - scale rate (dEdy `outer` x)
              w'   = W wB' wN'
              -- bundle of derivatives for next step
              dWs  = tr wN #> dEdy
          in  (w' :~ n', dWs)

Compiler, O Where Art Thou?

  • Haskell is all about the compiler helping guide you write your code. But how much did the compiler help there?
  • How can the “shape” of the matrices guide our programming?
  • We basically rely on naming conventions to make sure we write our code correctly.

Haskell Red Flags

  • How many ways can we write the function and have it still typecheck?
  • How many of our functions are partial?

A Typed Alternative

data Weights i o = W { wBiases :: !(R o)
                     , wNodes  :: !(L o i)
                     }

An o x i layer

A Typed Alternative

From HMatrix:

R :: Nat -> Type
L :: Nat -> Nat -> Type

An R 3 is a 3-vector, an L 4 3 is a 4 x 3 matrix.

Operations are typed:

(+)  :: KnownNat n               => R n   -> R n -> R n
(<#) :: (KnownNat m, KnownNat n) => L m n -> R n -> R m

KnownNat n lets hmatrix use the n in the type. Typed holes can guide our development, too!

Data Kinds

With -XDataKinds, all values and types are lifted to types and kinds.

In addition to the values True, False, and the type Bool, we also have the type 'True, 'False, and the kind Bool.

In addition to : and [] and the list type, we have ': and '[] and the list kind.

Data Kinds

ghci> :t True
Bool
ghci> :k 'True
Bool
ghci> :t [True, False]
[Bool]
ghci> :k '[ 'True, 'False ]
[Bool]

A Typed Alternative

data Network :: Nat -> [Nat] -> Nat -> Type where
    O    :: !(Weights i o)
         -> Network i '[] o
    (:~) :: KnownNat h
         => !(Weights i h)
         -> !(Network h hs o)
         -> Network i (h ': hs) o
infixr 5 :~
h1 :: Weight 10 8
h2 :: Weight 8  5
o  :: Weight 5  2

            O o :: Network 5  '[]     2
      h2 :~ O o :: Network 8  '[5]    2
h1 :~ h2 :~ O o :: Network 10 '[8, 5] 2
h2 :~ h1 :~ O o -- type error

Running

runLayer :: (KnownNat i, KnownNat o)
         => Weights i o
         -> R i
         -> R o
runLayer (W wB wN) v = wB + wN #> v

runNet :: (KnownNat i, KnownNat o)
       => Network i hs o
       -> R i
       -> R o
runNet (O w)     !v = logistic (runLayer w v)
runNet (w :~ n') !v = let v' = logistic (runLayer w v)
                      in  runNet n' v'

Exactly the same! No loss in expressivity!

Running

Much better! Matrices and vector lengths are guaranteed to line up!

Also, note that the interface for runNet is better stated in its type. No need to reply on documentation.

runNet
    :: (KnownNat i, KnownNat o)
    => Network i hs o -> R i -> R o

The user knows that they have to pass in an R i, and knows to expect an R o.

Generating

randomWeights :: (MonadRandom m, KnownNat i, KnownNat o)
              => m (Weights i o)
randomWeights = do
    s1 :: Int <- getRandom
    s2 :: Int <- getRandom
    let wB = randomVector  s1 Uniform * 2 - 1
        wN = uniformSample s2 (-1) 1
    return $ W wB wN

No need for explicit arguments! User can demand i and o. No reliance on documentation and parameter orders.

Generating

But, for generating nets, we have a problem:

randomNet :: forall m i hs o. (MonadRandom m, KnownNat i, KnownNat o)
          => m (Network i hs o)
randomNet = case hs of [] -> ??

Pattern matching on types

The solution for pattern matching on types: singletons.

-- (not the actual impelentation)

data Sing :: Bool -> Type where
    SFalse :: Sing 'False
    STrue  :: Sing 'True

data Sing :: [k] -> Type where
    SNil  :: Sing '[]
    SCons :: Sing x -> Sing xs -> Sing (x ': xs)

data Sing :: Nat -> Type where
    SNat :: KnownNat n => Sing n

Pattern matching on types

ghci> :t SFalse
Sing 'False
ghci> :t STrue `SCons` (SFalse `SCons` SNil)
Sing '[True, False]
ghci> :t SNat @1 `SCons` (SNat @2 `SCons` SNil)
Sing '[1, 2]

Random networks

randomNet' :: forall m i hs o. (MonadRandom m, KnownNat i, KnownNat o)
           => Sing hs -> m (Network i hs o)
randomNet' = \case
    SNil            ->    O <$> randomWeights
    SNat `SCons` ss -> (:~) <$> randomWeights <*> randomNet' ss

Implicit passing

Explicitly passing singletons can be ugly.

class SingI x where
    sing :: Sing x

We can now recover the expressivity of the original function, and gain demand-driven shapes.

Implicit passing

randomNet :: forall i hs o m. (MonadRandom m, KnownNat i, SingI hs, KnownNat o)
          => m (Network i hs o)
randomNet = randomNet' sing

Now the shape can be inferred from the functions that use the Network.

We can also demand them explicitly:

randomNet @1 @'[8,5] @2

Backprop

train :: forall i hs o. (KnownNat i, KnownNat o)
      => Double           -- ^ learning rate
      -> R i              -- ^ input vector
      -> R o              -- ^ target vector
      -> Network i hs o   -- ^ network to train
      -> Network i hs o
train rate x0 target = fst . go x0

Ready for this?

Backprop

    go  :: forall j js. KnownNat j
        => R j              -- ^ input vector
        -> Network j js o   -- ^ network to train
        -> (Network j js o, R j)
    -- handle the output layer
    go !x (O w@(W wB wN))
        = let y    = runLayer w x
              o    = logistic y
              -- the gradient (how much y affects the error)
              --   (logistic' is the derivative of logistic)
              dEdy = logistic' y * (o - target)
              -- new bias weights and node weights
              wB'  = wB - konst rate * dEdy
              wN'  = wN - konst rate * (dEdy `outer` x)
              w'   = W wB' wN'
              -- bundle of derivatives for next step
              dWs  = tr wN #> dEdy
          in  (O w', dWs)
    -- handle the inner layers
    go !x (w@(W wB wN) :~ n)
        = let y          = runLayer w x
              o          = logistic y
              -- get dWs', bundle of derivatives from rest of the net
              (n', dWs') = go o n
              -- the gradient (how much y affects the error)
              dEdy       = logistic' y * dWs'
              -- new bias weights and node weights
              wB'  = wB - konst rate * dEdy
              wN'  = wN - konst rate * (dEdy `outer` x)
              w'   = W wB' wN'
              -- bundle of derivatives for next step
              dWs  = tr wN #> dEdy
          in  (w' :~ n', dWs)

Backprop

    -- handle the inner layers
    go !x (w@(W wB wN) :~ n)
        = let y          = runLayer w x
              o          = logistic y
              -- get dWs', bundle of derivatives from rest of the net
              (n', dWs') = go o n
              -- the gradient (how much y affects the error)
              dEdy       = logistic' y * dWs'
              -- new bias weights and node weights
              wB'  = wB - konst rate * dEdy
              wN'  = wN - konst rate * (dEdy `outer` x)
              w'   = W wB' wN'
              -- bundle of derivatives for next step
              dWs  = tr wN #> dEdy
          in  (w' :~ n', dWs)

Surprise! It’s actually identical! No loss in expressivity.

Also, typed holes can help you write your code in a lot of places. And shapes are all verified.

By the way, still waiting for linear types in GHC :)

Type-Driven Development

The overall guiding principle is:

  1. Write an untyped implementation.
  2. Realize where things can go wrong:
    • Partial functions?
    • Many, many ways to implement a function incorrectly with the current types?
    • Unclear or documentation-reliant API?
  3. Gradually add types in selective places to handle these.

I recommend not going the other way (use perfect type safety before figuring out where you actually really need them). We call that “hasochism”.

Further reading